A zonotope is the Minkowski sum of finitely many line segments:
Z=l1+l2+...+ln
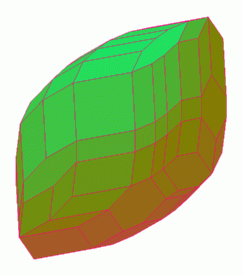
A "typical" zonotope, in this case a sum of 14 line segments, is displayed on the right.
There are many equivalent definitions. Another algebraic definition closely related to ours is to say that Z is the linear image of an hypercube in n-space. This is evident by writing the line segments as lk=[-1,1]ck (if we restrict to centered zonotopes for simplicity), and observing that then
Z=C [-1,1]n,
where C is a matrix with n column vectors ck and [-1,1]n is the centered hypercube in n-space. The matrix C can be used to represent Z on a computer. It is also convenient for working with linear images of zonotopes, because the zonotope TZ is represented by the matrix TC. See the Rigorous Dynamics page. For much more information on zonotopes, especially on their geometric characterization, can be found in The Geometry Junkyard.
Every face of a zonotope is again a zonotope. The collection of all faces which have a given line segment as a common summand form a band (or zone; etymology) around the zonotope. For less than four line segments, the zonotope Z is simply a line segment (n=1), a parallelogram (n=2) or a parallelepiped (n=3). For more than three segments, the geometry is more complex. Check out the Online Zonotope Builder and Viewer.